二叉树遍历
以一定的顺序规则,逐个访问二叉树的所有结点,这个过程就是二叉树的遍历。
// 构造二叉树
function TreeNode(val) {
this.val = val;
this.left = this.right = null;
}
// root
const root = new TreeNode('A');
// left node
const leftNode = new TreeNode('B');
root.left = leftNode;
leftNode.left = new TreeNode('D');
leftNode.right = new TreeNode('E');
// right node
const rightNode = new TreeNode('C');
root.right = rightNode;
rightNode.right = new TreeNode('F');
// 二叉树数据结构
// root = {
// val: "A",
// left: {
// val: "B",
// left: {
// val: "D"
// },
// right: {
// val: "E"
// }
// },
// right: {
// val: "C",
// right: {
// val: "F"
// }
// }
// };
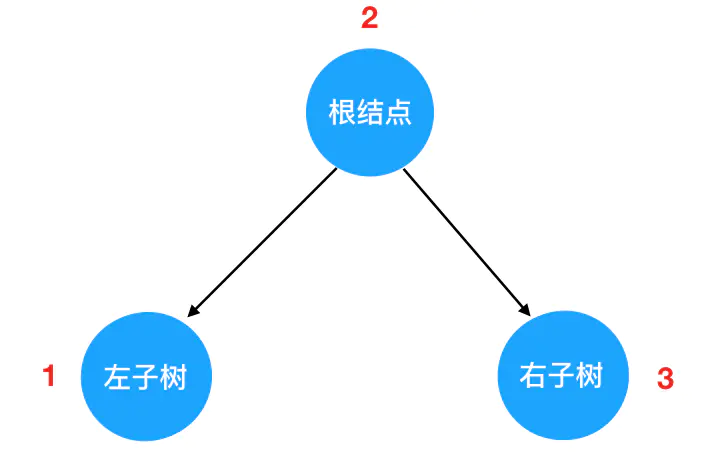
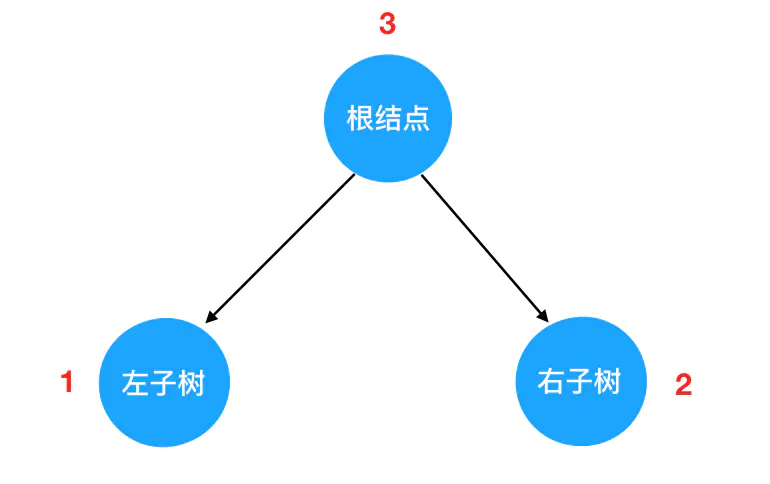
由于二叉树都是由三部分组成的:根节点、左子树、右子树。而且左右子树都是二叉树,因此可以将子树也「分解」看作由这个基本结构组成的。因此对树的遍历,就可以看做是对这三个部分的遍历。
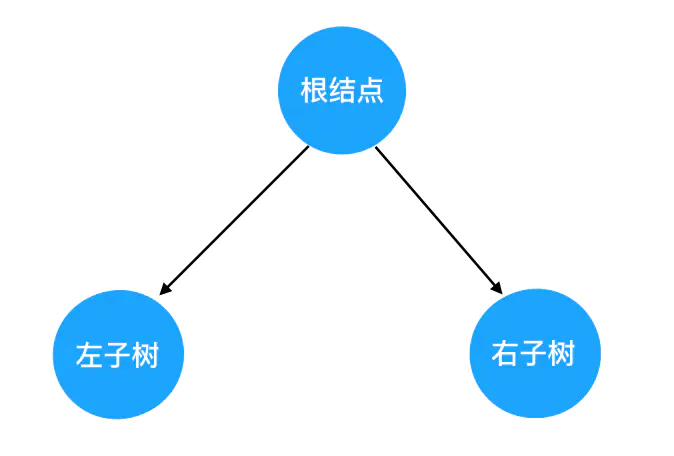
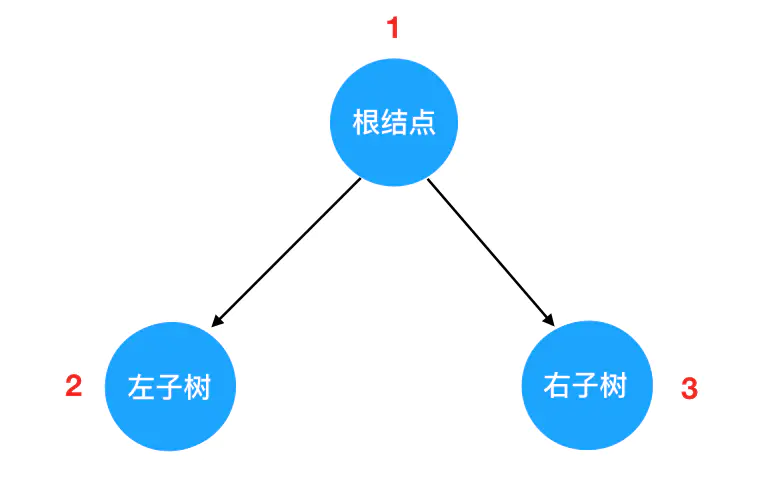
按照实现方式的不同,遍历方式又可以分为以下两种:
- 递归遍历:基于根结点的遍历分别被安排在了首要位置、中间位置和最后位置(根结点的遍历的时机),可以将递归遍历方法分为先序遍历、中序遍历、后序遍历
- 先序遍历:根结点 -> 左子树 -> 右子树
- 中序遍历:左子树 -> 根结点 -> 右子树
- 后序遍历:左子树 -> 右子树 -> 根结点
- 迭代遍历:层次遍历
递归遍历
Tip
编程语言中,函数直接或间接调用函数本身,则该函数称为递归函数。
先序遍历
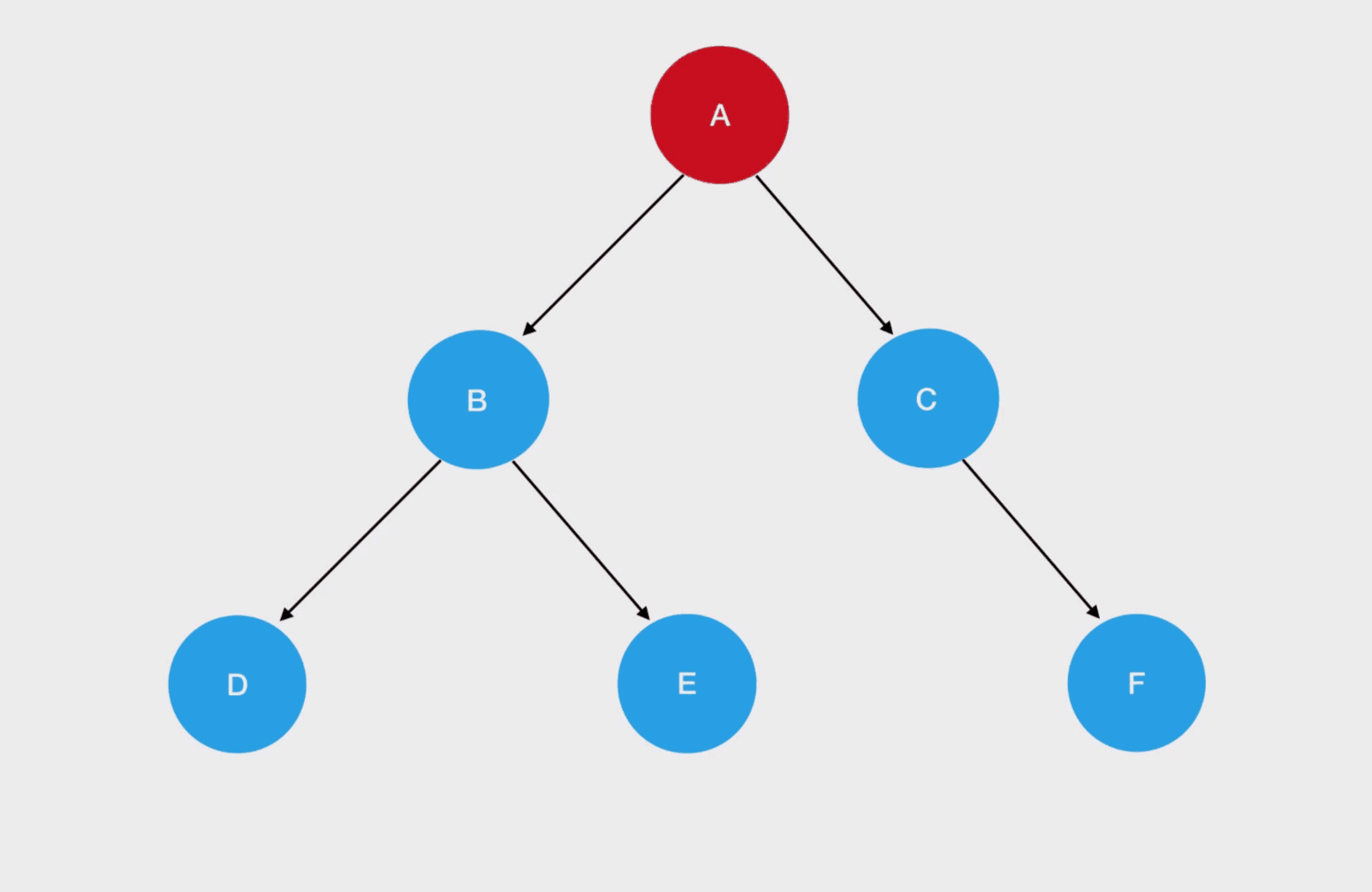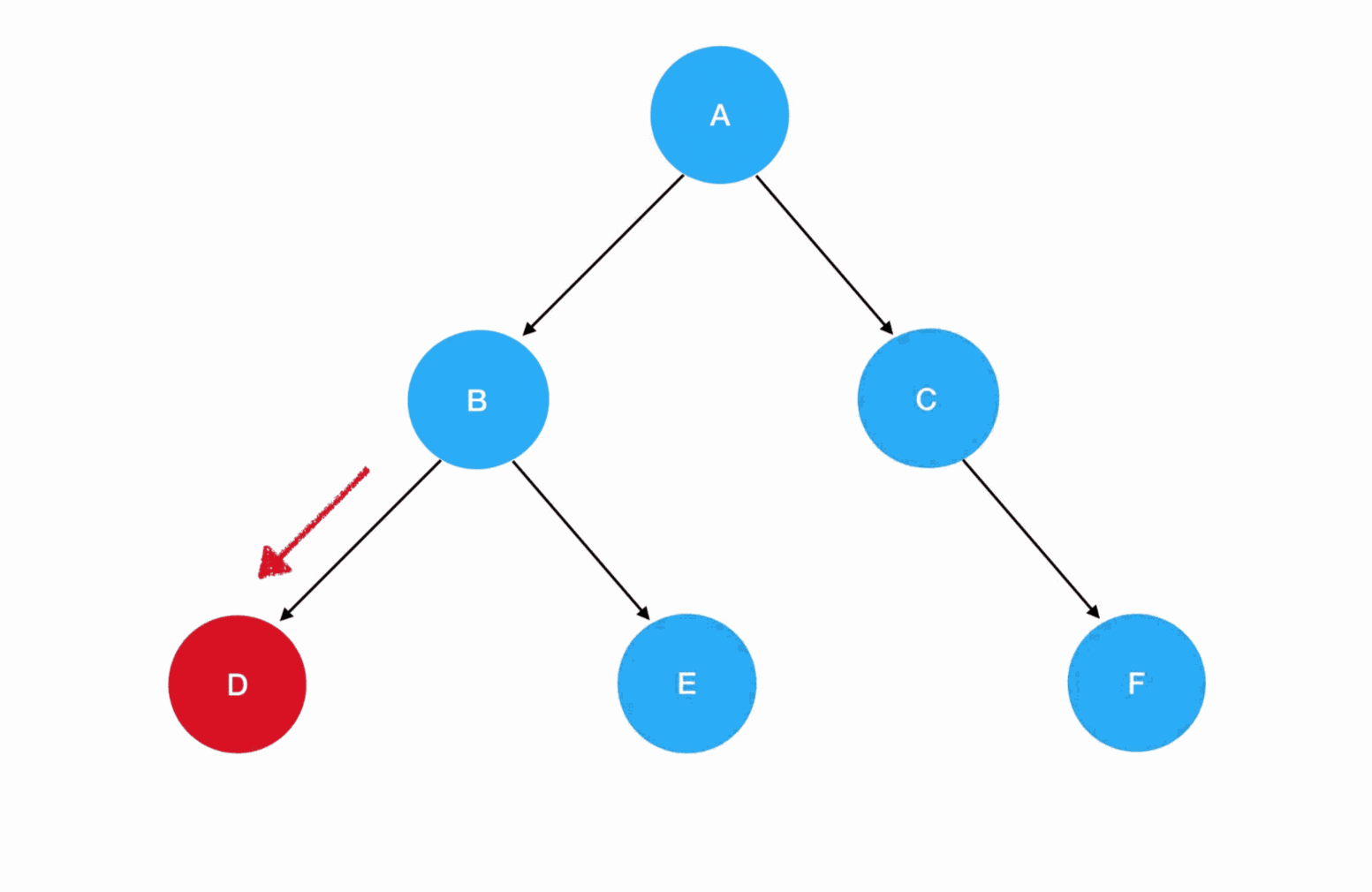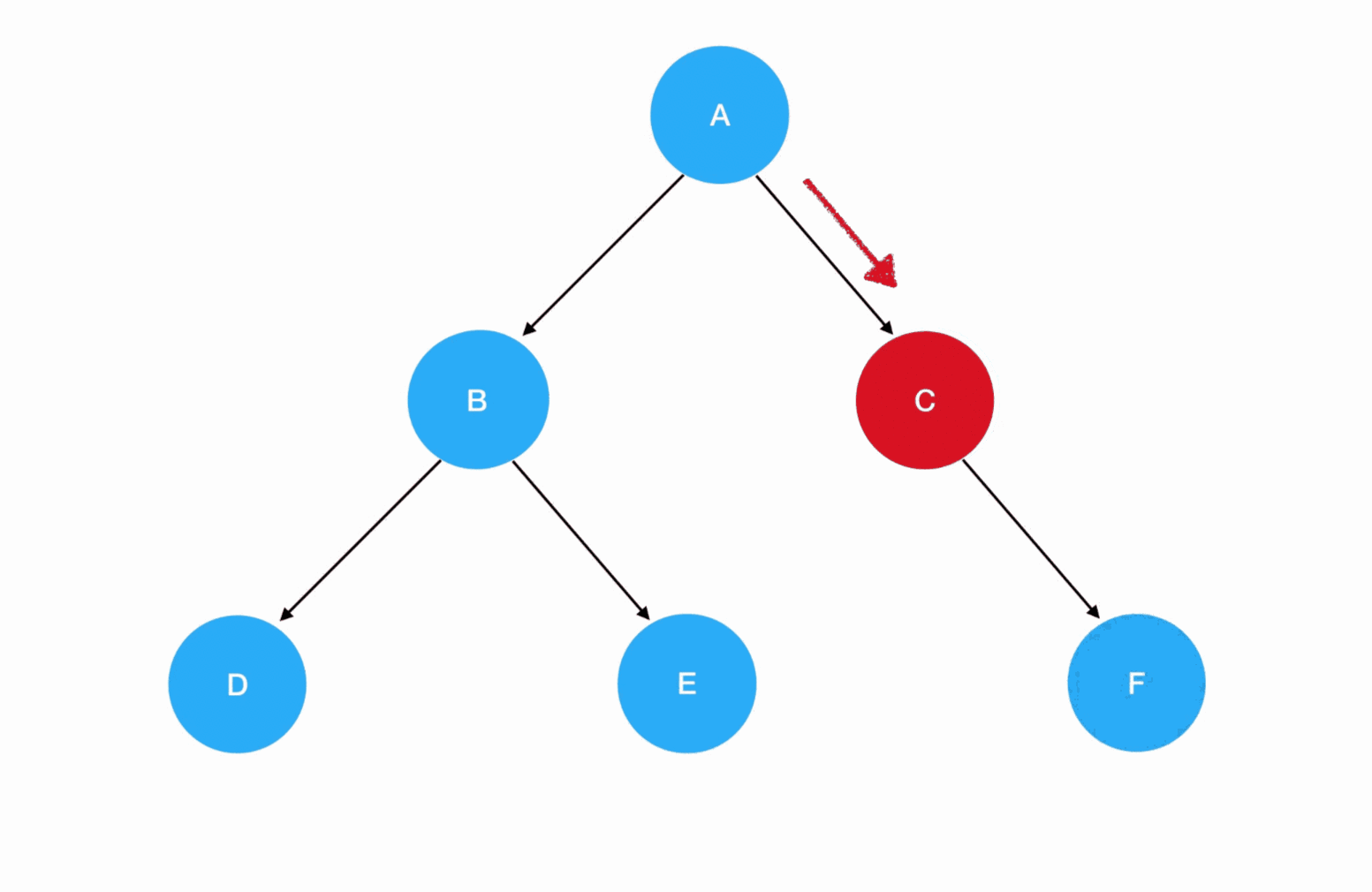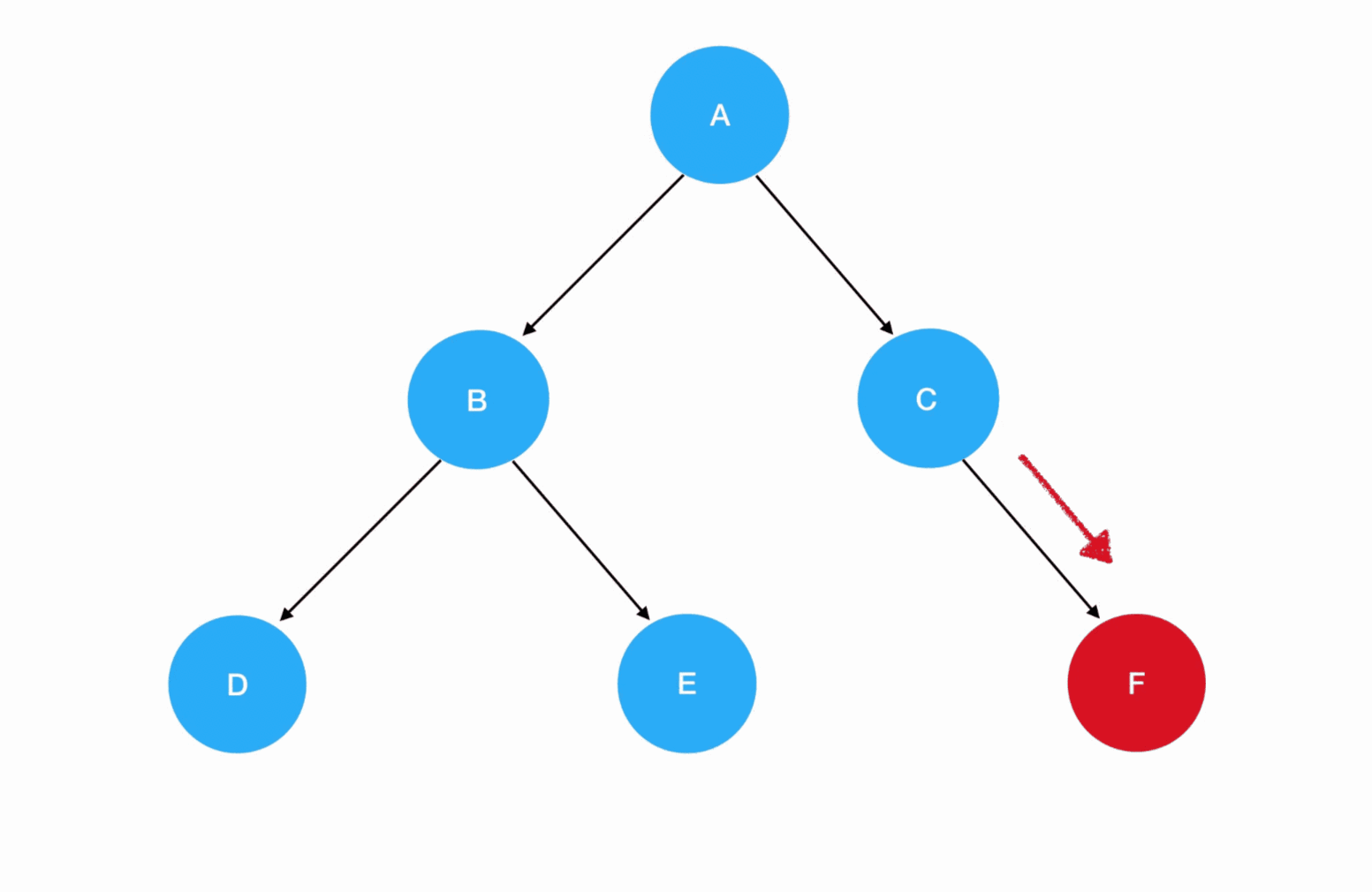
- 先序遍历的递归式:每一次重复的内容是
根结点 -> 左子树 -> 右子树 - 先序遍历的递归边界:当我们发现遍历的目标树为空的时候,停止递归调用
// 先序遍历函数
// 入参是树的根结点对象
funciton preorder(root) {
if(root) {
// 输出当前遍历的结点值
console.log('当前遍历的结点值是:', root.val);
// 递归遍历左子树
preorder(root.left);
// 递归遍历右子树
preorder(root.right);
} else {
// 递归边界,当结点为空时返回
return
}
}
// 运行结果
preorder(root);
// 当前遍历的结点值是: A
// 当前遍历的结点值是: B
// 当前遍历的结点值是: D
// 当前遍历的结点值是: E
// 当前遍历的结点值是: C
// 当前遍历的结点值是: F
中序遍历
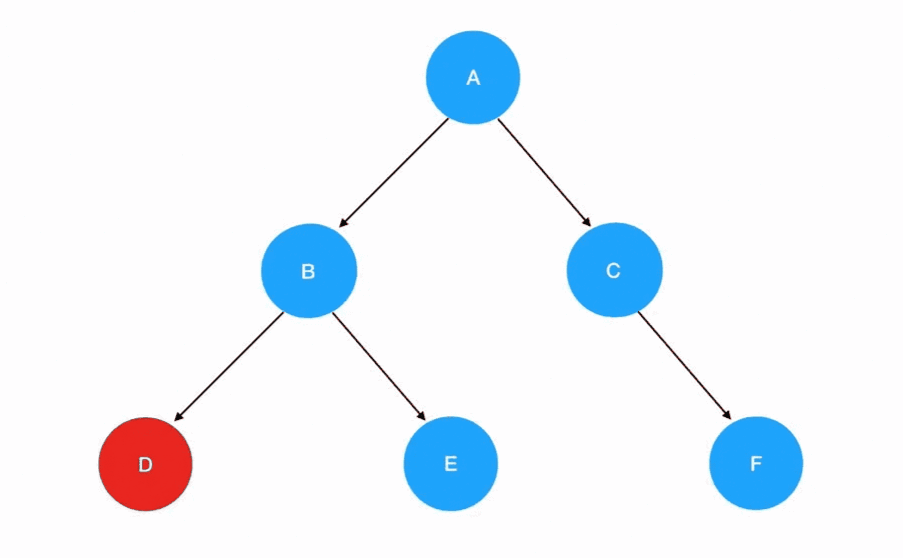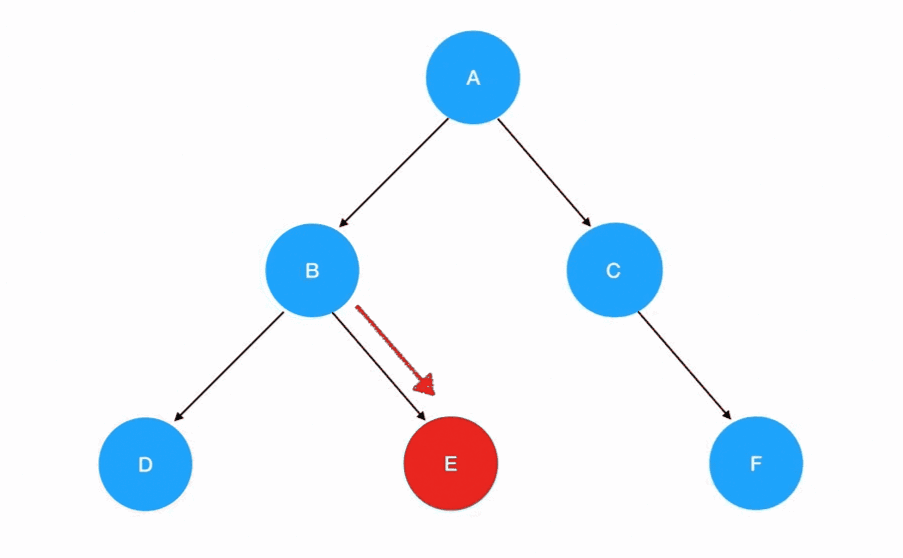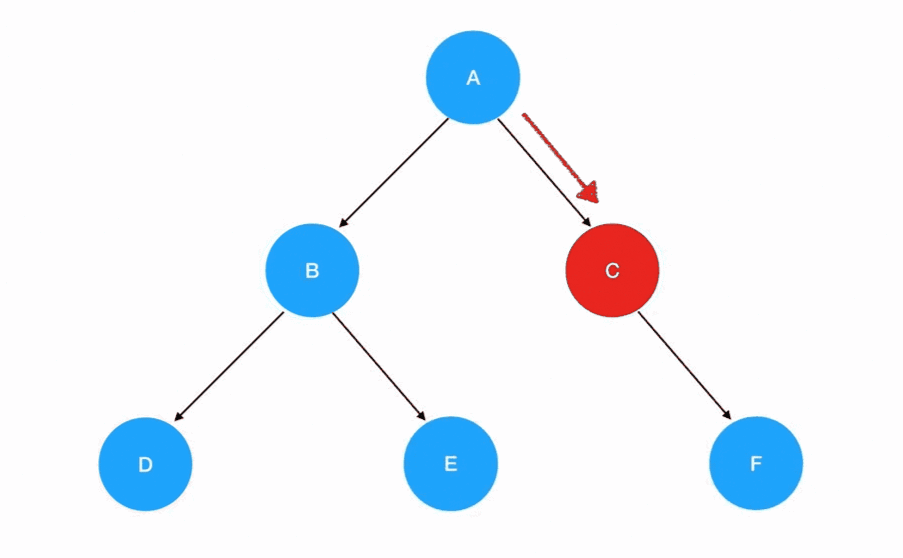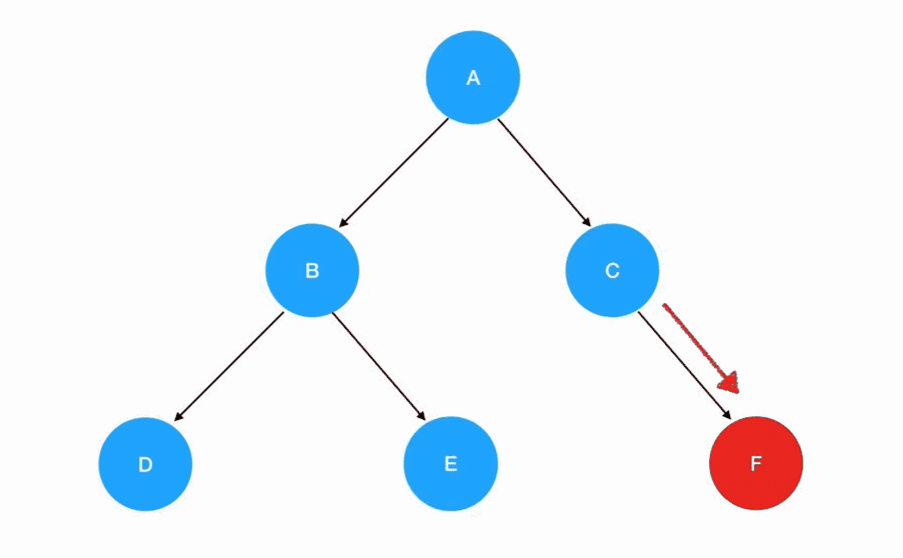
- 中序遍历的递归式:每一次重复的内容是
左子树 -> 根结点 -> 右子树 - 中序遍历的递归边界:当我们发现遍历的目标树为空的时候,停止递归调用
💡 与先序遍历的唯一发生改变的是递归式里调用递归函数的顺序,左子树的访问会优先于根结点
// 中序遍历函数
// 入参是树的根结点对象
function inOrder(root) {
if (root) {
// 递归遍历左子树
inOrder(root.left);
// 输出当前遍历的结点值
console.log('当前遍历的结点值是:', root.val);
// 递归遍历右子树
inOrder(root.right);
} else {
// 递归边界,当结点为空时返回
return
}
}
// 运行结果
inOrder(root);
// 当前遍历的结点值是: D
// 当前遍历的结点值是: B
// 当前遍历的结点值是: E
// 当前遍历的结点值是: A
// 当前遍历的结点值是: C
// 当前遍历的结点值是: F
后序遍历
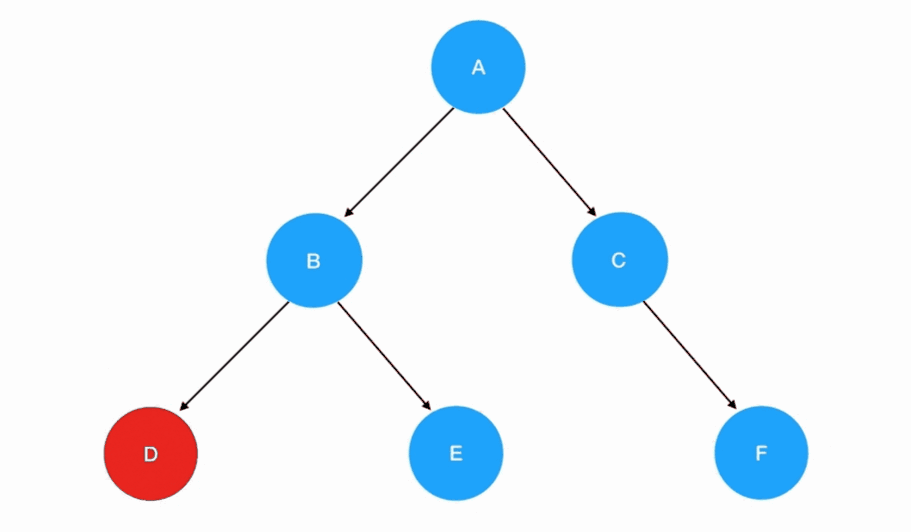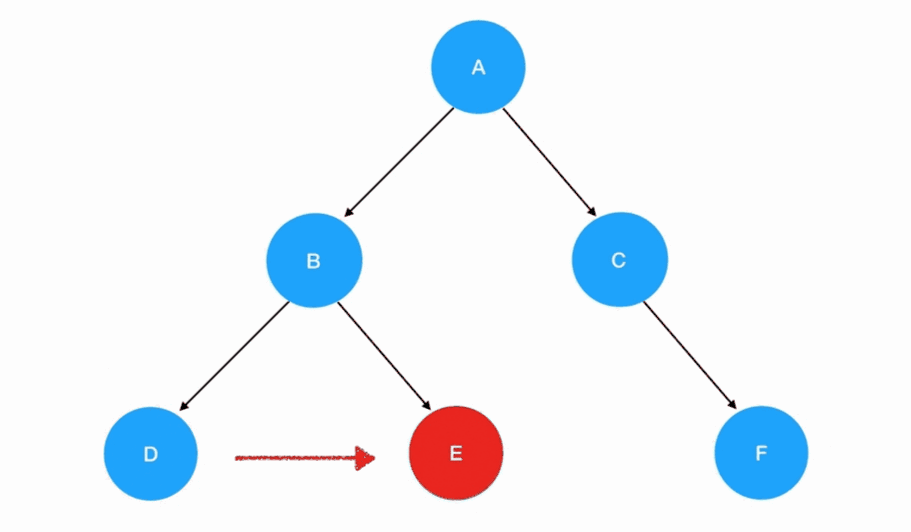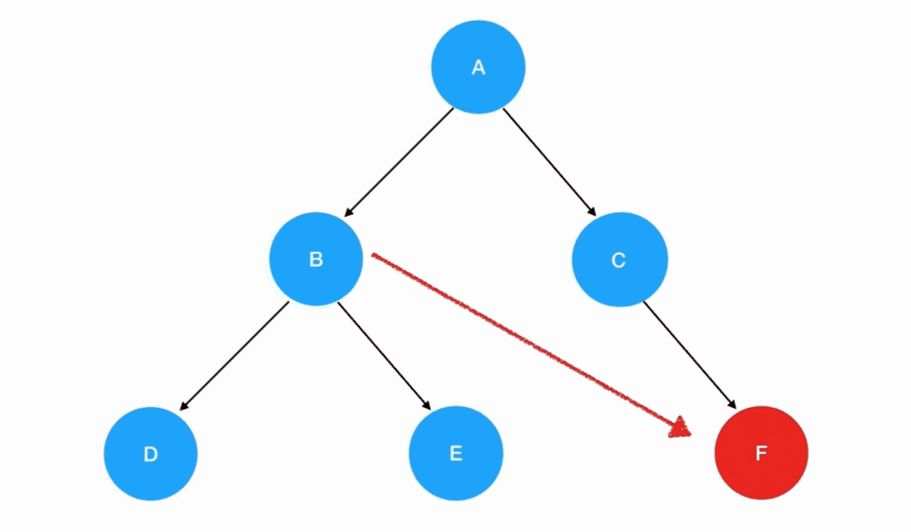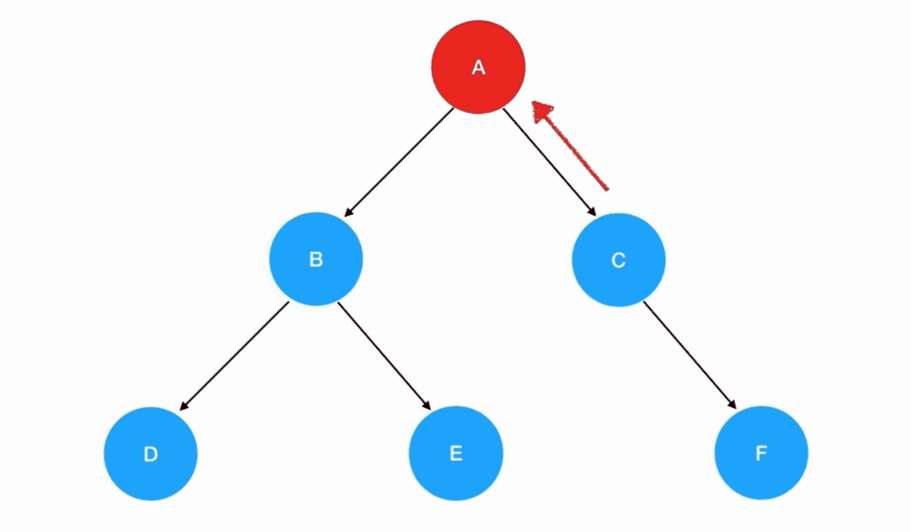
- 后序遍历的递归式:每一次重复的内容是
左子树 -> 右子树 -> 根结点 - 后序遍历的递归边界:当我们发现遍历的目标树为空的时候,停止递归调用
💡 与先序遍历的唯一发生改变的是递归式里调用递归函数的顺序,左子树和右子树的访问会优先于根结点
// 后序遍历函数
// 入参是树的根结点对象
function postOrder(root) {
if(root) {
// 递归遍历左子树
postOrder(root.left);
// 递归遍历右子树
postOrder(root.right);
// 输出当前遍历的结点值
console.log('当前遍历的结点值是:', root);
} else {
// 递归边界,当结点为空时返回
return
}
}
// 运行结果
postOrder(root);
// 当前遍历的结点值是: D
// 当前遍历的结点值是: E
// 当前遍历的结点值是: B
// 当前遍历的结点值是: F
// 当前遍历的结点值是: C
// 当前遍历的结点值是: A
迭代遍历
先序遍历
题目描述:给定一个二叉树,返回它的前序(先序)遍历序列。
示例: 输入: 1,null,2,3
md1 \ 2 / 3输出: 1,2,3
Tip
一个思维工具:递归和栈有着脱不开的干系,当可以用递归做出来的题,而需要使用其他解法,此时我们本能地往栈上想。
题目中的出参是一个数组(结点的值),它可以看作是是一个栈的出栈序列,因此只需要合理地安排结点入栈和出栈的时机,使结点出栈序列符合二叉树的前序遍历规则即可。

前序遍历的规则是 先遍历根结点、然后遍历左树、最后遍历右树,这正是我们所期望的出栈序列;而按道理入栈序列和出栈序列相反, 即按道理结点入栈应该按照 右->左->根 的顺序,⚠️ 但我们先接触到的起点就是根结点,因此第一步需要将根结点执行一次先入栈,然后马上出栈的操作,保证第一次出栈是根节点。
然后就在每一轮迭代中取出栈顶的元素(后 push 入栈的结点)作为当前的根结点,将值添加到结果数组,并将其右、左子树 push 到栈中,这样就可以构成所需的栈元素层叠关系,将根元素和左树先输出,后输出右树。
先序迭代遍历的出入栈顺序:
- 将当前根结点入栈
- 取出栈顶结点,将结点值
push进结果数组 - 若栈顶结点有右孩子,则将右孩子入栈(当下下轮的结点的根结点)
- 若栈顶结点有左孩子,则将左孩子入栈(当下一轮的结点的根结点)
重复 2、3、4 步骤,通过 push 和 pop(前期会交替执行 push 和 pop 操作,后期只有一直执行 pop 操作) 操作直至栈空,遍历完整个二叉树。
/**
*
* @param {TreeNode} root
* @return {number[]}
*/
const preorderTraversal = function (root) {
// 初始化结果数组
let res = [];
// 初始化栈结构
let stack = [];
// 迭代边界条件
if (!root) {
return res;
}
// 首先将根节点入栈
stack.push(root);
// 进行迭代,当栈不为空就不断重复入栈、出栈操作
while (stack.length) {
// 将栈顶结点出栈,作为当前的根节点
let cur = stack.pop();
// 将结点值 push 到结果数组的尾部
res.push(cur.val);
// 若当前子树有右孩子,先将其入栈
if (cur.right) {
stack.push(cur.right);
}
// 若当前子树有左孩子,后将其入栈
if (cur.left) {
stack.push(cur.left);
}
}
// 返回结果数组
return res;
}