链表应用
做链表处理类问题要把握住一个中心思想:处理链表结点之间的指针关系。
结合实际面试中的命题规律,题目分为以下三类:
- ⭐ 链表的处理:合并、删除等
- 链表的反转及其衍生题目
- 链表成环问题及其衍生题目
链表的合并
真题描述:将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有结点组成的。
示例:输入:
1->2->4,1->3->4输出:1->1->2->3->4->4
两个链表如果想要合并为一个链表,我们恰当地补齐双方之间结点 next 指针的指向关系,就能达到目的。新建一个链表 head(第一个结点,作为进入点),然后赋值给 cur 作为为指针,基于结点值 val 的大小对两个链表进行穿针引线。
还要考虑两个链表长度不等的情况,若其中一个链表已经完全被串进新链表里了,而另一个链表还有剩余结点,考虑到该链表本身就是有序的,我们可以直接把它整个拼到目标链表的尾部。
/**
* @param {ListNode} l1
* @param {ListNode} l2
* @return {ListNode}
*/
let l1 = {
val: 1,
next: {
val: 2,
next: {
val: 4,
next: null
}
}
};
let l2 = {
val: 1,
next: {
val: 3,
next: {
val: 4,
next: null
}
}
};
let resultList = mergeTwoLists(l1, l2);
while(resultList) {
console.log(resultList.val); // 1->1->2->3->4->4
resultList = resultList.next;
}
function mergeTwoLists(l1, l2) {
// 创建新链表,定义头结点确保链表可以被访问到
let head = new ListNode();
// cur 表示当前指针所在的位置
// 初始化 cur 指针
let cur = head;
while (l1 && l2) {
// 如果 l1 的结点值较小,先用指针先串起 l1 的结点
if (l1.val <= l2.val) {
cur.next = l1;
// l1 向前一步
l1 = l1.next;
}
// 如果 l2 的结点值较小,先用指针先串起 l2 的结点
else {
cur.next = l2;
// l2 向前一步
l2 = l2.next
}
// 指针「串起」一个结点后,也向前一步
cur = cur.next;
}
// 处理链表不等长的情况
cur.next = l1 === null ? l2 : l1;
// 返回起始点
return head;
}
function ListNode(val) {
this.node = val;
this.next = null;
}
链表结点的删除
真题描述:给定一个排序链表,删除所有重复的元素,使得每个元素只出现一次。
示例 1:输入:
1->1->2输出:1->2示例 2:输入:1->1->2->3->3输出:1->2->3
链表的删除是一个基础且关键的操作,只需要删除将目标结点的前驱结点 next 指针往后指一格即可。由于此处是已排序的链表,直接在遍历中依次判断前后两个元素值是否相等即可。
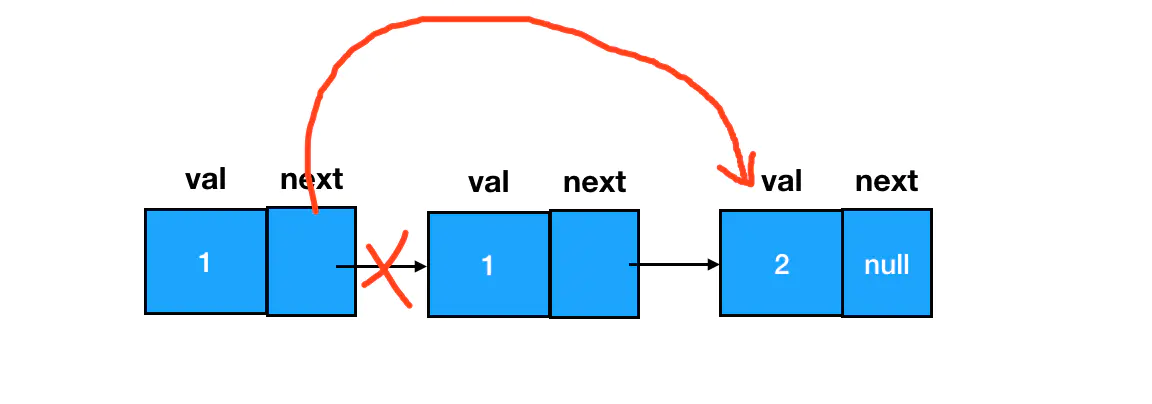
/**
* @param {ListNode} head
* @return {ListNode}
*/
let l1 = {
val: 1,
next: {
val: 1,
next: {
val: 2,
next: null
}
}
}
let l2 = {
val: 1,
next: {
val: 1,
next: {
val: 2,
next: {
val: 3,
next: {
val: 3,
next: null
}
}
}
}
}
l1 = deleteDuplicates(l1);
l2 = deleteDuplicates(l2);
while (l1) {
console.log(l1.val);
l1 = l1.next;
}
console.log("------");
while (l2) {
console.log(l2.val);
l2 = l2.next;
}
function deleteDuplicates(list) {
// 指针
// 初始化指针为链表第一个结点
let cur = list;
// 指针遍历结点
while (cur && cur.next) {
// 若当前结点和它后面一个结点值相等(重复)
if (cur.val === cur.next.val) {
// 删除靠后的那个结点(去重)
cur.next = cur.next.next;
} else {
// 若不重复,继续遍历
cur = cur.next
}
}
// 返回去重后的链表(第一个结点,链表进入点0
return list
}
dummy 结点
真题描述:给定一个排序链表,删除所有含有重复数字的结点,只保留原始链表中 没有重复出现的数字。
示例 1:输入:
1->2->3->3->4->4->5输出:1->2->5示例 2:输入:1->1->1->2->3输出:2->3
该问题是删除问题的延伸,一般将前驱结点的 next 指针往后挪一位「跳跃」跨过一个结点即可实现结点的删除,但是如果要将出现的重复的结点都删除,至少要删除两个结点才行,而且必须保证前驱结点有结点指向才可以,经常会遇到这样的问题:链表的第一个结点,因为没有前驱结点,导致我们面对它无从下手。这时我们就可以用一个 dummy 结点来解决这个问题。
dummy 结点:就是人为制造出来的链表的第一个结点的前驱结点,这样链表中所有的结点都能确保有一个前驱结点,也就所有结点都能够用同样的逻辑来处理了。
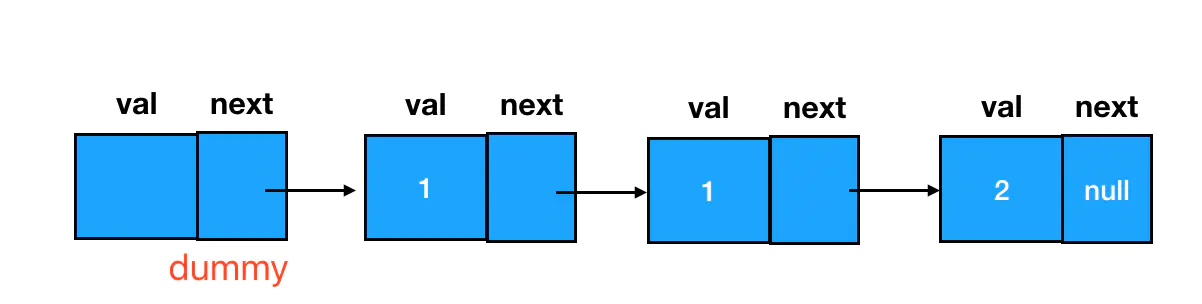
let l1 = {
val: 1,
next: {
val: 2,
next: {
val: 3,
next: {
val: 3,
next: {
val: 4,
next: {
val: 4,
next: {
val: 5,
next: null
}
}
}
}
}
}
};
let l2 = {
val: 1,
next: {
val: 1,
next: {
val: 1,
next: {
val: 2,
next: {
val: 3,
next: null
}
}
}
}
};
l1 = deleteDuplicates(l1);
l2 = deleteDuplicates(l2);
while (l1) {
console.log(l1.val);
l1 = l1.next;
}
console.log("------");
while (l2) {
console.log(l2.val);
l2 = l2.next;
}
function deleteDuplicates(head) {
// 极端情况:0个或1个结点,则不会重复,直接返回
if (!head || !head.next) {
return head
}
// 创建 dummy 结点
let dummy = new ListNode();
// 将 dummy 连接到原始链表的首个节点上
dummy.next = head;
// 创建指针
// 初始化指向为首个结点
let cur = dummy;
// 遍历结点,从虚拟结点 dummy 开始,其值 dummy.val 为 undefined
// 当前结点后还有两个结点时
while (cur.next && cur.next.next) {
// 判断后面两个结点的值是否相同
if (cur.next.val === cur.next.next.val) {
// 如果两个结点的值相同,记下该重复值
let value = cur.next.val;
// 反复地排查后面的元素是否存在多次重复该值的情况
while (cur.next && cur.next.val === value) {
// 若有,则删除
cur.next = cur.next.next;
}
} else {
// 若不重复,遍历下一个结点
cur = cur.next;
}
}
// 返回处理后的链表的首个结点(非 dummy 结点)
return dummy.next;
}
function ListNode(val) {
this.val = val;
this.next = null;
}
Tip
dummy 结点可以帮我们处理头结点为空的边界问题,帮助我们简化解题过程。因此涉及链表操作、尤其是涉及结点删除的题目(对前驱结点的存在性要求比较高),建议直接把 dummy 给用起来,建立好的编程习惯:
const dummy = new ListNode()
// 这里的 head 是链表原有的第一个结点
dummy.next = head
快慢指针
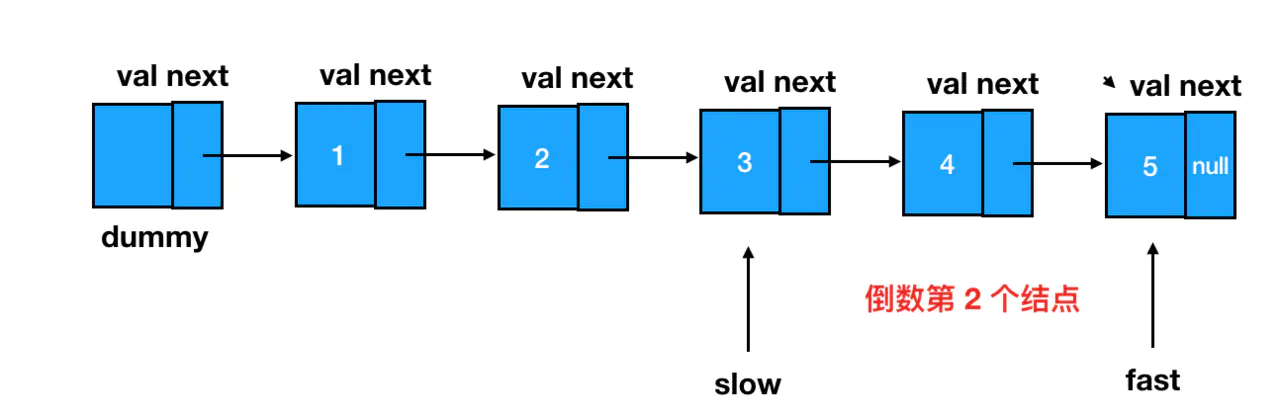
真题描述:给定一个链表,删除链表的倒数第
n个结点,并且返回链表的头结点。示例: 给定一个链表:
1->2->3->4->5,和n = 2。当删除了倒数第二个结点后,链表变为1->2->3->5,💡 给定的n保证是有效的。
由于链表不能像数组一样通过属性 length 和索引来直接定位到结点,只能通过遍历来访问结点和了解结点数量。而遍历不可能从后往前走,因此倒数第 N 个结点可以转换为(正数)第 M = len - n + 1 个结点,这里 len 代表链表的总长度。
可以直接遍历两趟:第一趟设置一个变量 count = 0,每遍历到一个不为空的结点 count + 1 ,一直遍历到链表结束为止,得出链表的总长度 len;根据这个总长度,通过公式 M = len - n + 1 算出倒数第 n 个结点到底对应正数第几个结点。然后第二趟遍历到第 M - 1(也就是 len - n,因为遍历计数变量一般从 0 开始) 个结点的时候就可以停下来,执行删除操作,将前驱结点指向后驱结点,这样就可以删除中间结点。
但是两次遍历时间复杂度较大,可以使用双指针的快慢指针来优化。原来的解法需要使用两次遍历实现求长度,做减法 和 找定位,而使用快慢指针就可以将做减法和找定位这个过程给融合。
快慢指针指的是两个一前一后的指针,由于它们「起步」位置不同造成的,但是「步速」一样,两个指针可以在一次遍历中往同一个方向走,前一个快指针控制遍历的终点(停止时机),后一个慢指针用来执行删除操作。通过快指针先行一步、接着快慢指针一起前进这个操作,巧妙地把两个指针之间的差值保持在了 n 上,💡 用空间换时间,本质上其实就是对关键信息进行提前记忆,相当于用两个指针对差值实现了记忆。
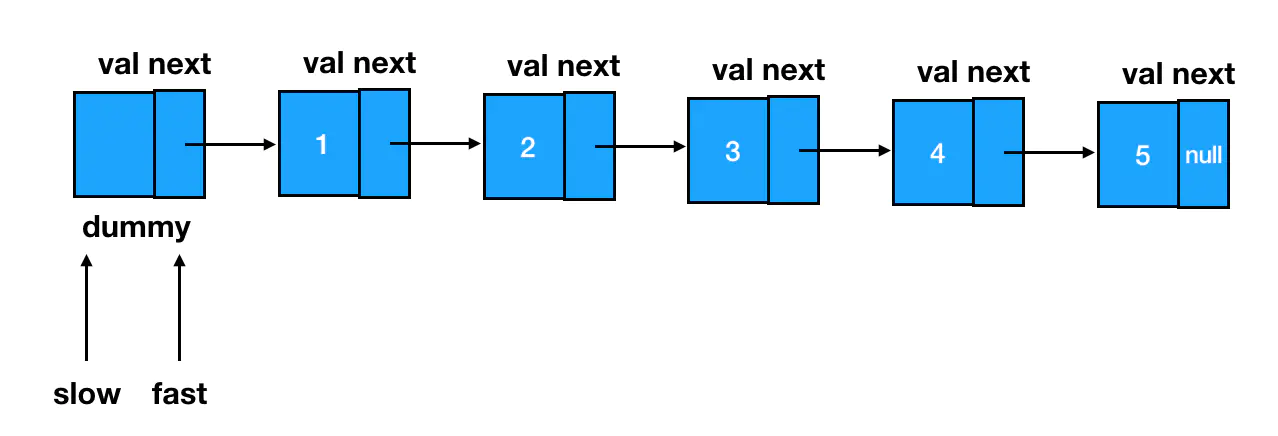
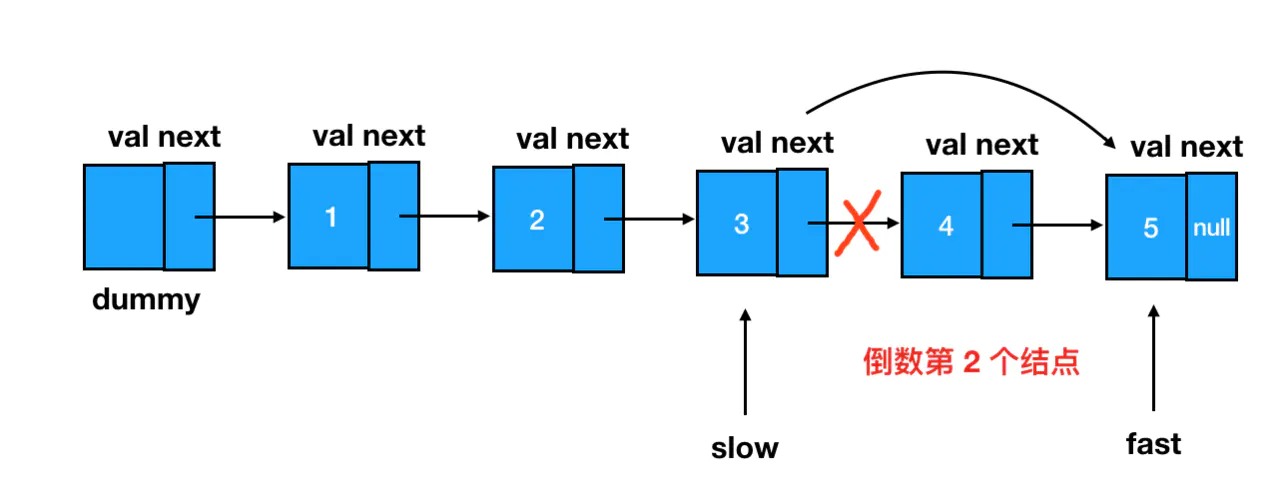
根据需要删除的位置为倒数第 n 个结点来设定快慢指针的间距
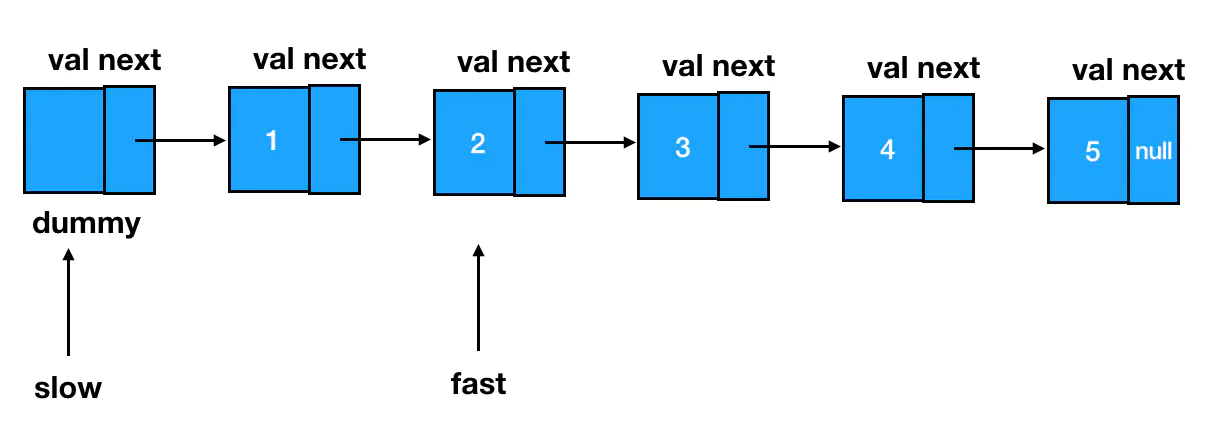
当快指针走到链表末尾(第 len 个)时,慢指针刚好就在 len - n 这个位置上。
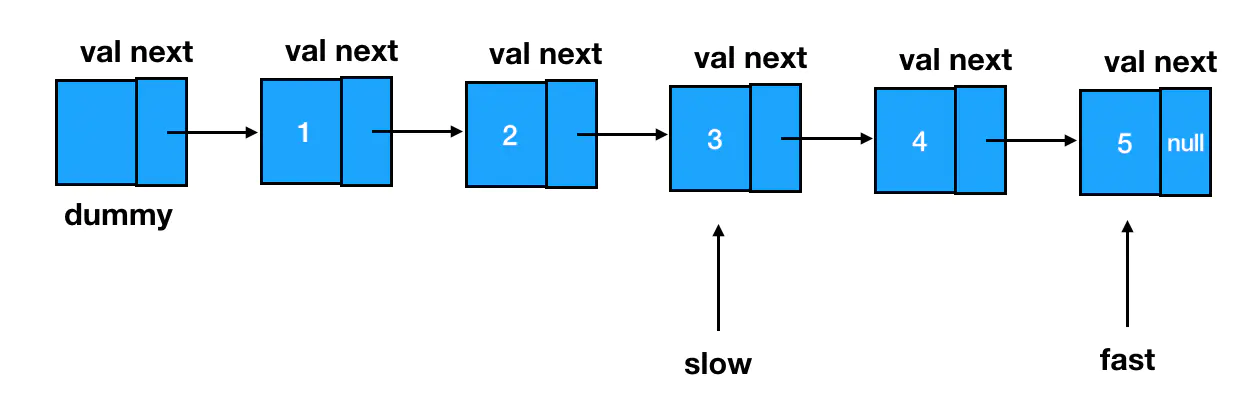
function removeNthFromEnd(head, n) {
// 创建 dummy 结点
const dummy = new ListNode();
// 指向原始链表的开始结点
dummy.next = head;
// 初始化快慢指针,均指向 dummy 结点
let fast = dummy;
let slow = dummy;
// 基于删除结点的位置设置快慢指针的间距
// 快指针先走 n 步
while (n !== 0) {
fast = fast.next;
n--
}
// 遍历链表
while (fast.next) {
fast = fast.next;
slow = slow.next;
}
// 快指针到达了最后结点,删除慢指针此时指代结点的后继结点
slow.next = slow.next.next;
// 返回处理后链表的头节点
return dummy.next;
}
function ListNode(val) {
this.val = val;
this.next = null;
}
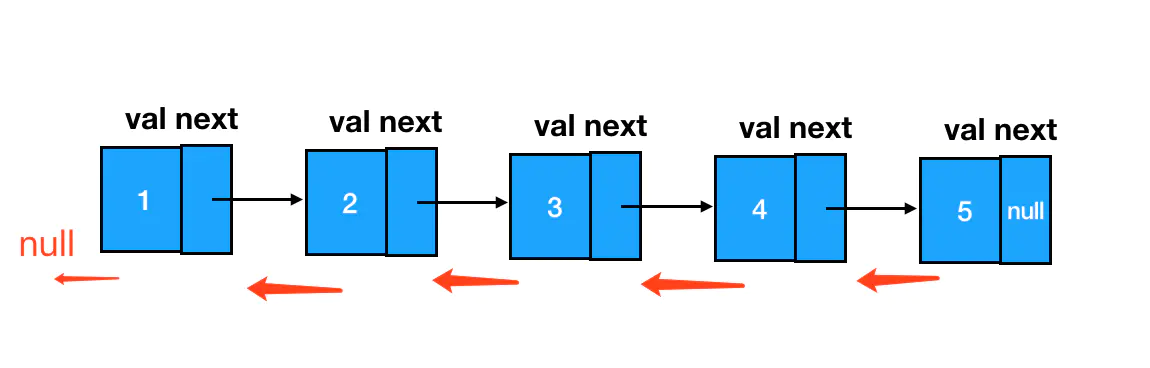
链表翻转
真题描述:定义一个函数,输入一个链表的头结点,反转该链表并输出反转后链表的头结点。
示例:输入:
1->2->3->4->5->NULL输出:5->4->3->2->1->NULL
处理链表的本质,是处理链表结点之间的指针关系,只要想办法把每个结点 next 指针的指向给反过来就行。
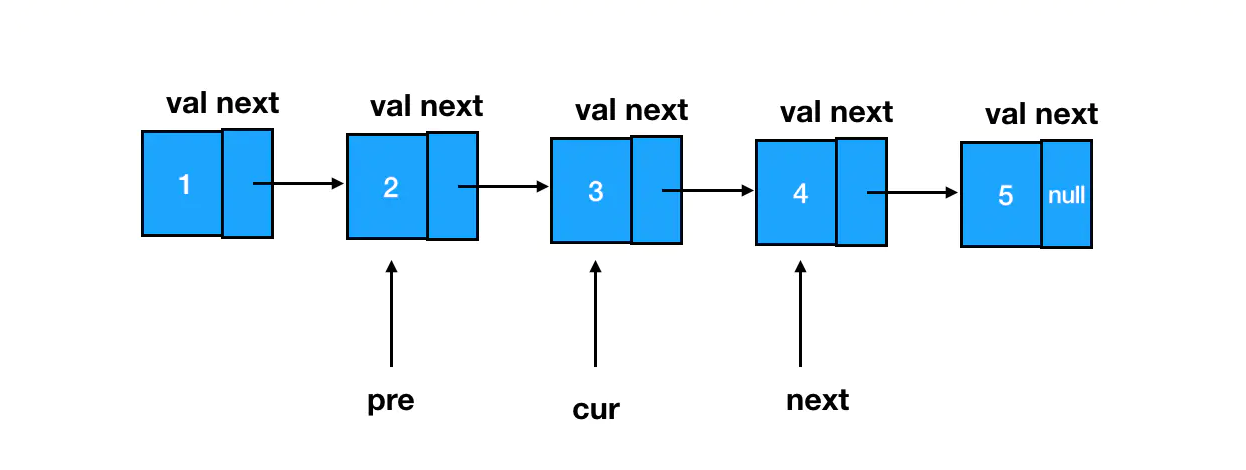
这里我们需要用到三个指针,它们分别指向目标结点 cur、目标结点的前驱结点 pre、目标结点的后继结点 next。这里我只需要一个简单的 cur.next = pre,就做到了目标结点的 next 指针的反转,指向前驱结点,而 next 保留着目标结点原来的后继结点,以便访问和遍历。
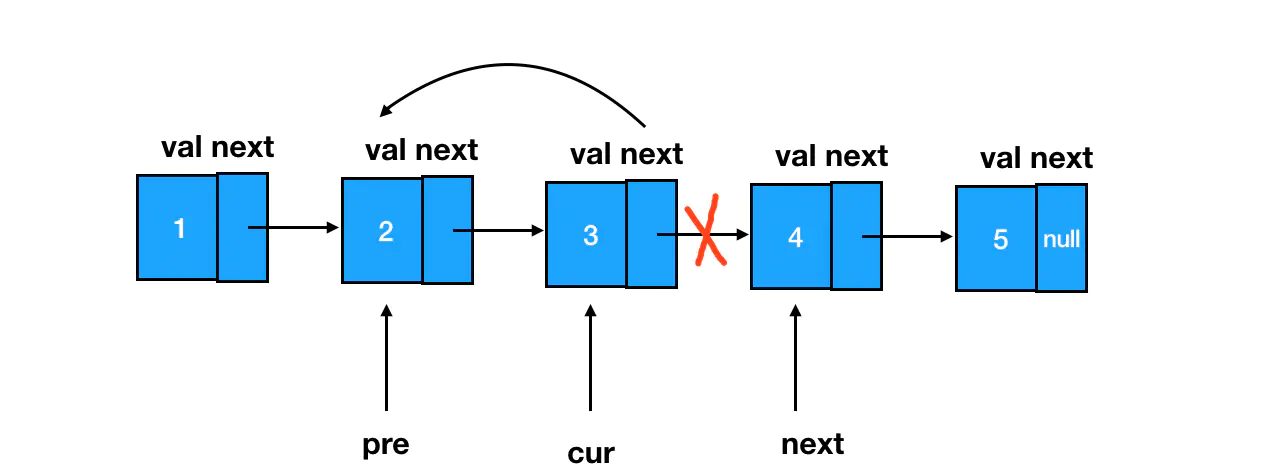
/**
* @param {ListNode} head
* @return {ListNode}
*/
function reverseList(head) {
// 初始化前驱结点和目标结点
let pre = null;
let cur = head;
while (cur !== null) {
// 记录当前结点原来的后继结点
let next = cur.next;
// 反转指针
cur.next = pre;
// 遍历链表
// 指针向前走一步,直至 cur 为 null
pre = cur;
cur = next;
}
// 返回反转后的链表,指针 pre 是新链表的头结点
return pre;
}
局部翻转
真题描述:反转从位置
m到n的链表。请使用一趟扫描完成反转。💡1 ≤ m ≤ n ≤ 链表长度。示例:输入:
1->2->3->4->5->NULL,m = 2,n = 4输出:1->4->3->2->5->NULL
局部链表翻转除了要处理指定部分结点的 next 指针指向问题,还需要处理被逆序的区间前后的两个结点的 next 指针问题。
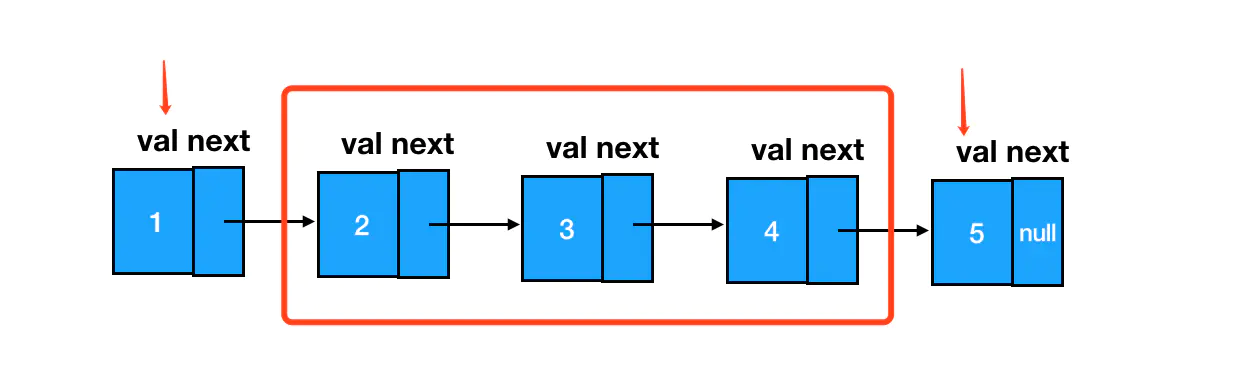
由于我们遍历链表的顺序是从前往后遍历,那么为了避免前面结点(区间头部结点和区间前的结点)随着遍历向后推进被遗失,我们需要提前把区间前的这两个结点缓存下来。而区间后的结点就没有这么麻烦,随着遍历的进行,当我们完成了区间内的指针反转后,此时 cur 指针就恰好指在区间后的结点上。
最后只需要将区间前的结点的 next 指针指向翻转后区间内的头结点,同时翻转前区间内的头结点的 next 指针指向区间后的结点即可将区间和外部结点「串」起来。
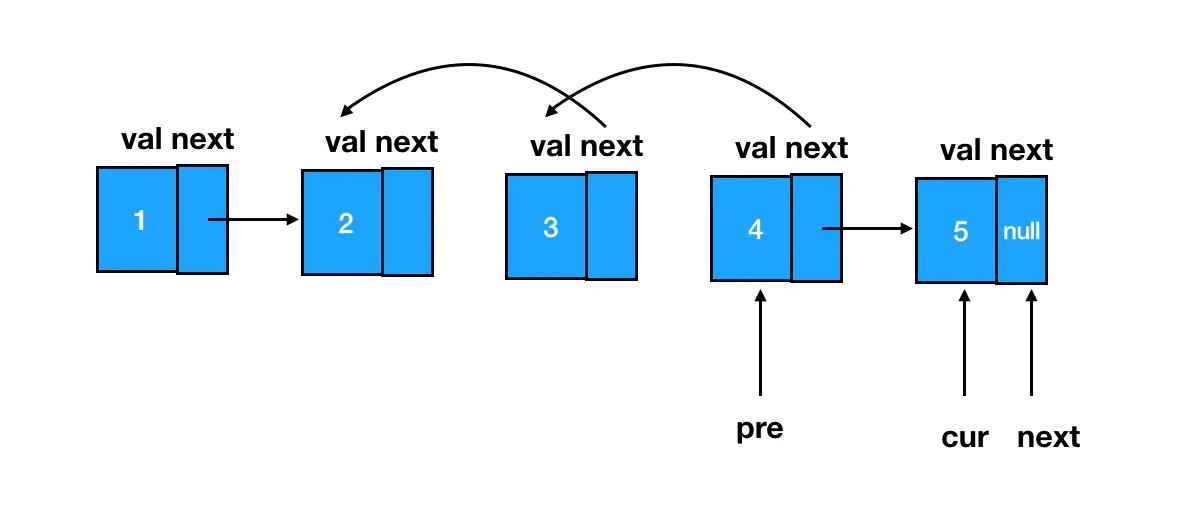
/**
* @param {ListNode} head
* @param {number} m
* @param {number} n
* @return {ListNode}
*/
function reverseBetween(head, m, n) {
// 定义 pre、cur、leftHead 指针
// 其中 pre、cur 是翻转区间结点时使用的指针
// 用 leftHead 来承接整个区间的前驱结点
let pre, cur, leftHead
// 考虑区间包含头结点的情况,需要使用 dummy 结点
const dummy = new ListNode();
dummy.next = head;
// 创建一个游标 p,用于遍历,初始化指向 dummy
let p = dummy;
// 往前走 m-1 步,到达区间的前驱结点
for(let i=0; i<m-1; i++) {
p = p.next;
}
// 指针 leftHead 记录下这个结点
leftHead = p;
// 定义 start 指针记录原来区间的第一个结点
let start = leftHead.next;
pre = start;
cur = pre.next;
// 遍历翻转区间内的结点
// 直至 pre 指向区间内最后的结点,cur 指向区间的后继结点
for(let i=m; i<n; i++) {
// 记录当前结点的后继结点
let next = cur.next;
cur.next = pre;
// 向前走一步
pre = cur;
cur = next;
}
// 将区间的前驱结点指向翻转后的区间第一个结点
leftHead.next = pre;
// 将翻转后的区间的最后一个结点指向区间的后继结点
start.next = cur;
// 返回修改后链表的头结点
return dummy.next;
}
function ListNode(val) {
this.val = val;
this.next = null;
}
判断链表成环
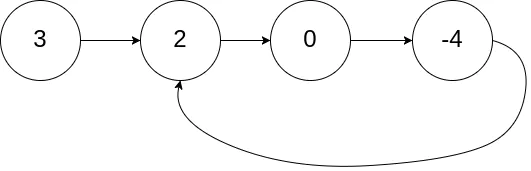
真题描述:给定一个链表,判断链表中是否有环。
示例 1:输入:
[3,2,0,4](链表结构如下图) 输出:true即链表中存在一个环链表成环
一个环形链表是能够让遍历它的游标回到原点,为走过的结点都「打上」标签 flag,即从 flag 出发只要能够再回到 flag 处,那么就意味着正在遍历一个环形链表。
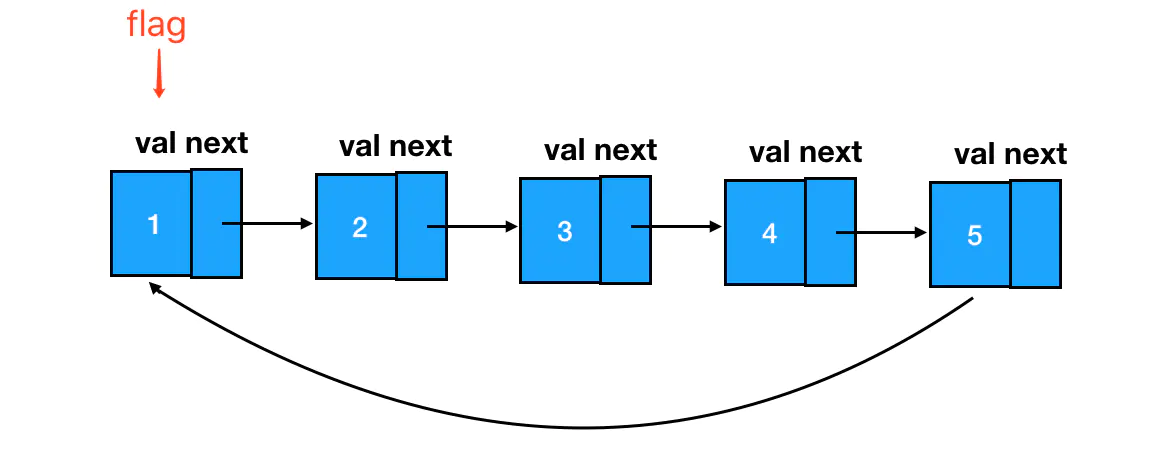
/**
* @param {ListNode} head
* @return {boolean}
*/
function hasCycle(head) {
// 如果存在结点就继续遍历
while (head) {
// 判断当前结点是否已打 flag
if (head.flag) {
// 如果已打 flag 证明链表成环
return true;
} else {
// 如果不存在 flag 就打上标签
head.flag = true;
// 往前走一步
head = head.next;
}
}
// 默认返回 false
return false;
}
Tip
这道题还有一个公认的比较经典的思路,就是用快慢指针来做:定义慢指针 slow,快指针 fast。两者齐头并进,slow 一次走一步、fast 一次走两步。这样如果它们是在一个有环的链表里移动,一定有相遇的时刻,
当移动的次数为 t 时,slow 移动的路程就是t,fast 移动的路程为2t,假如环的长度为 s,那么当下面这个条件满足时:
// 如果刚好指针距离覆盖链表环的长度
2t - t = s
// 此时
t = s
slow 和 fast 就一定会相遇。反之,如果两者没有相遇,同时 fast 遍历到了链表的末尾,发现 next 指针指向 null,则链表中不存在环。
定位环形链表的环起点
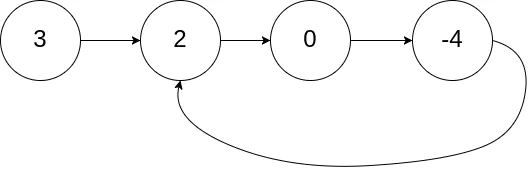
真题描述:给定一个链表,返回链表开始入环的第一个结点。 如果链表无环,则返回 null。
示例 1:输入:
head = [3,2,0,-4](如下图) 输出:tail connects to node index 1即链表中有一个环,其尾部连接到第二个结点。示例1 示例 2:输入:
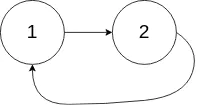
head = [1,2](如下图)输出:tail connects to node index 0即链表中有一个环,其尾部连接到第一个结点。示例2 示例 3:输入:
head = [1](如下图)输出:no cycle即链表中没有环。示例3
如果一个结点是环形链表成环的起点,那么它一定是第一个被发现 flag 标志已存在的结点,将对应的结点返回即可。
/**
* @param {ListNode} head
* @return {ListNode}
*/
function detectCycle(head) {
// 如果有节点就继续遍历
while(head) {
if(head.flag) {
// 存在 flag 证明就是成环
// 返回第一次碰到的 flag 对应的结点
return head;
} else {
head.flag = true;
head = head.next;
}
}
return null;
}